Graph Theory I - Hoang Anh Duc - MIM - HUS - VNU

Graph Theory II - Hoang Anh Duc - MIM - HUS - VNU

Work 15 (I).

Prove that if $G$ is a simple undirected graph with exactly 2 vertices $u, v$ with odd degree then these vertices belongs to a single connected component of $G$.

Solution:

• Vertices with odd degree: By the handshaking lemma, the number of vertices with odd degrees must be even. Given $G$ has exactly two vertices $u$ and $v$ with odd degrees, there can be no other vertices in $G$ with odd degree.
• Structure of $G$: If $u$ and $v$ does not belong to the same connected component. then $u$ and $v$ would lie in different connected components of $G$.
  • Consider the connected component $C_1$ containing $u$. Since $u$ has an odd degree, the sum of degress of all vertices in $C_1$ would be odd, violating the handshaking lemma (as the sum of all degrees in any graph or subgraph must be even).
  • Similarly, the connected component $C_2$ containing $v$ would also have an odd degree sum, which again violates the handshaking lemma.
• The contradiction implies that $u$ and $v$ cannot lie in separate connected components. Therefore, $u$ and $v$ must belong to the same connected component.

Work 20 (I).

Prove that:

Are true for all undirected connected graph $G = (V, E)$.

Solution:

(1):

• Consider the minimum degree of a vertex in $G$, denoted as $\delta(G) = \min_{v \in V} \deg_G(v)$.
• Removing a vertex $v$ disconnects it from its neighbors. Since $v$ has exactly $\deg_G(v)$ neighbors, at most $\deg_G(v)$ vertices are directly affected when $v$ is removed.
• The vertex connectivity $\kappa (G)$ cannot exceed $\delta (G)$, because the removal of any single vertex affects at most $\deg_g(v)$ vertices.
• Therefore: $\kappa(G) \leq \min_{v \in V} \deg_G(v)$.

(2):

• Removing all edges incident to a vertex $v$ will isolate $v$ from the rest of the graph. The number of edges incident to $v$ is $\deg_G (v)$.
• The edge connectivity $\lambda (G)$ is the minimum of edges required to disconnect $G$. Clearly, $\lambda(G)$ cannot exceed $\delta (G)$, because disconnecting $G$ by removing edges must involve at least as many edges as are incident to the vertex with the smallest degree.
• Therefore: $\lambda(G) \leq \min_{v \in V} \deg_G(v)$.

Work 21 (I).

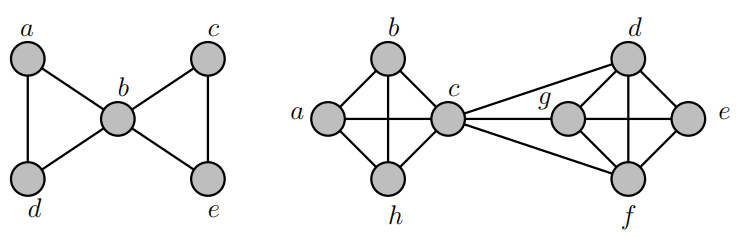
Find $\kappa(G)$, $\lambda(G)$ and $\min_{v \in V} \deg(v)$ for:

Solution:

• Graph (1)
  • $\kappa(G) = 2$.
  • $\lambda(G) = 2$.
  • $\min_{v \in V} \deg(v) = 2$.
• Graph (2)
  • $\kappa(G) = 3$.
  • $\lambda(G) = 3$.
  • $\min_{v \in V} \deg(v) = 3$.

Work 24 (I).

Find the number of paths with length $n$ between two distinct vertices of $K_4$ with $n$ being 2, 3, 4 and 5.

Solution: 2, 6, 14, 36.

Work 2 (II).

With what value of $n$ does the graphs $K_n$, $C_n$, $W_n$ and $Q_n$ has an Eulerian circuit.

Solution:

• $K_n$: $n$ is odd.
• $C_n$: $n \geq 3$.
• $W_n$: $n$ is even.
• $Q_n$: $n$ is even.

Work 4 (II).

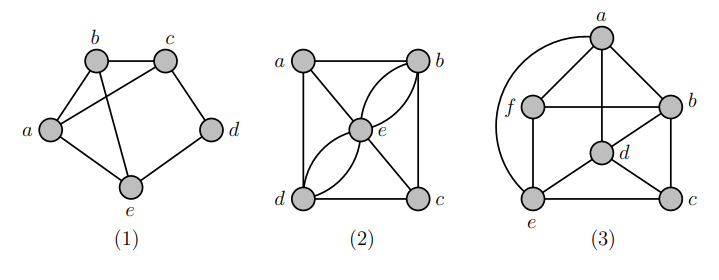
Find an Eulerian path/circuit in these graphs if any.

Solution:

• Graph (1)
  • Degrees for a, b, c, d, e: 3, 2, 3, 2, 2.
  • Odd vertices: a and c.
  • EP: Exists.
  • EC: None.
• Graph (2)
  • Degrees for a, b, c, d, e: 2, 3, 3, 2, 4.
  • Odd vertices: b and c.
  • EP: Exists.
  • EC: None.
• Graph (3)
  • Degrees for a, b, c, d, e, f: 4, 4, 4, 4, 4, 4.
  • Odd vertices: None
  • EP: Exists.
  • EC: Exists.

Work 6 (II).

Give a graph where it’s Eulerian circuit is also a Hamilton circuit.

Solution: $C_3$

Work 7 (II).

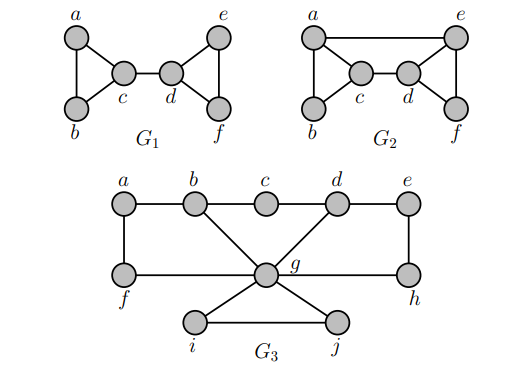
Which of the following graphs has a Hamilton circuit and why.

Solution:

• Graph (1)
  • HC: Exists: a -> b -> e -> d -> c -> a.
• Graph (2)
  • HC: None.
• Graph (3)
  • HC: Exists: a -> e -> c -> d -> b -> f -> a.