Table of Content

Multinomial Logistic Regression

Given dataset \(X = \{ (x_i, y_i) \}_{i=1}^N\) where \(x_i \in \mathbb{R}^n\) and \(y_i \in \{ 1,2,\ldots,C \}\), the Multinomial Logistic Regression model states that the likelihood of the input \(x\) belonging to class \(y=c\) is:

\[P(y = c \mid x, \Theta, \mathcal{B}) = \frac{\exp(z_c)}{\sum^C_\kappa \exp(z_\kappa)} \space ; \quad z_\kappa = x^T \theta_\kappa + \beta_\kappa \quad\]

• Where \(\Theta = \{ \theta_1, \theta_2, \ldots, \theta_C \}\) are the weights and \(\mathcal{B} = \{ \beta_1, \beta_2, \ldots, \beta_C \}\) are the biases and they make up the model’s parameters.
• The set \(Z = \{ z_1, z_2, \ldots, z_C \}\) are called the logits for each of the \(C\) classes, which contains the linear combinations of the input \(x\) with the weights and biases.
• The expression \(\frac{\exp(z_c)}{\sum^C_\kappa \exp(z_\kappa)}\) is the \(c\)-th element of \(\mathcal{P} = \{ P(y=1 \mid x, \Theta, \mathcal{B}), \ldots, P(y=C \mid x, \Theta, \mathcal{B}) \}\) produced by the Softmax Function, in nature it maps the \(C\) linear combinations \(Z\) of the input \(x\) and the weights \(\Theta\) and biases \(\mathcal{B}\) to a probability distribution that sums up to 1. In other word, the softmax function takes \(Z \in \mathbb{R}^C\) and produces \(\mathcal{P} \in \mathbb{R}^C\) such that \(\sum_c^C P(y=c \mid x, \Theta, \mathcal{B}) = 1\).

Here is a visualization of the multinomial logistic regression model in the style of a neural network for queried input \(x_q\):

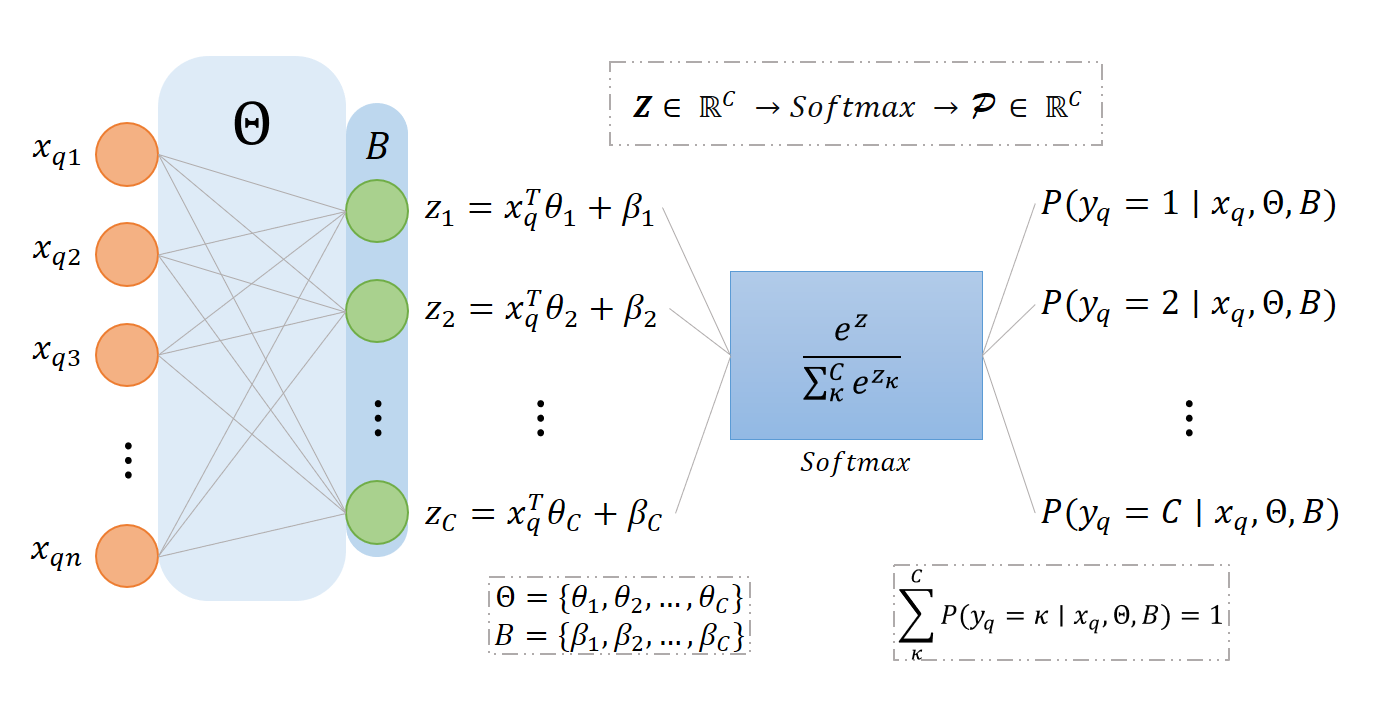
Our goal is to optimize the parameters \(\Theta\) and \(\mathcal{B}\), given MLE equation:

\[L(\Theta, \mathcal{B}) = \prod^N_{i=1} \prod^C_{c=1} \left( \frac{\exp(x_i^T \theta_c + \beta_c)}{\sum_{\kappa=1}^C \exp(x_i^T \theta_\kappa + \beta_\kappa)} \right)^{1[y_i=c]} \quad\]

• Where \(1[y_i=c]\) is an indicator function that equals 1 if \(y_i = c\) and 0 otherwise.

We take the Log Likelihood to simplify the calculation of MLE:

\[\begin{gather*} \log L(\Theta, \mathcal{B}) = \sum^N_{i=1} \sum_{c=1}^C 1[y_1=c] \log \left( \frac{\exp(x_i^T \theta_c + \beta_c)}{\sum_{\kappa=1}^C \exp(x_i^T \theta_\kappa + \beta_\kappa)} \right) \quad \\[15pt] = \sum^N_{i=1} \sum_{c=1}^C 1[y_1=c] \left( x_i^T \theta_c + \beta_c - \log \left( \sum_{\kappa=1}^C \exp(x_i^T \theta_\kappa + \beta_\kappa) \right) \right) \quad \end{gather*}\]

To maximize the MLE, we maximize the Log Likelihood, which is equivalent to minimizing the negative Log Likelihood, thus we define the cost function:

\[\begin{gather*} J(\Theta, \mathcal{B}) = -\frac{1}{N} \log L(\Theta, \mathcal{B}) \end{gather*}\]

We use Gradient Descent to solve the optimization problem iteratively:

• Step 1: Initialize parameters randomly: \(\Theta, \mathcal{B}\).
• Step 2: Calculate the Gradient of \(J(\Theta, \mathcal{B})\) with respect to each of the logit’s weights \(\theta_c\) and biases \(\beta_c\):

\[\begin{gather*} \frac{\partial J}{\partial \theta_c} = -\frac{1}{N} \sum_{i=1}^N \left(1[y_i=c] - \frac{\exp(x_i^T \theta_c + \beta_c)}{\sum_{\kappa=1}^C \exp(x_i^T \theta_\kappa + \beta_\kappa)}\right)x_i \quad \\[15pt] \frac{\partial J}{\partial \beta_c} = -\frac{1}{N} \sum_{i=1}^N \left(1[y_i=c] - \frac{\exp(x_i^T \theta_c + \beta_c)}{\sum_{\kappa=1}^C \exp(x_i^T \theta_\kappa + \beta_\kappa)}\right) \end{gather*}\]

These gradients will give us the direction of the weights and biases that will cause the steepest descent towards a local minima.

• Step 3: Update parameters:

\[\begin{gather*} \theta_c^{\text{new}} = \theta_c + \alpha \frac{\partial J}{\partial \theta_c} \quad \\[15pt] \beta_c^{\text{new}} = \beta_c + \alpha \frac{\partial J}{\partial \beta_c} \end{gather*}\]

Where \(\alpha\) denotes the learning rate. We perform step 2 and 3 for all logits from \(1\) to \(C\).

Often times, regularization is introduced to reduce overfitting, we will focus on L2 regularization, we implement it by simply adding a regularization term into the cost function:

\[J_{\text{reg}}(\Theta, \mathcal{B}) = -\frac{1}{N} \log L(\Theta, \mathcal{B}) + \frac{\lambda}{2N} \sum_{c=1}^C \| \theta_c \|^2_2 \quad\]

Where \(\lambda\) is a constant that represents the regularization strength. This will affect the weights of the model, large \(\lambda\) causes the weights to be closer to 0 and needs to be tune strategically to properly reduce overfitting. While the biases updates remain unchanged, our weights updates will be affected:

\[\theta_c^{\text{new}} = \theta_c + \alpha \frac{\partial J}{\partial \theta_c} - \frac{\lambda}{N} \theta_c \quad\]

Binary Logistic Regression

When there are \(C = 2\) classes, the softmax function is reduced to a special case called the Sigmoid Function, for simplicity we let \(y_i \in \{ 0, 1 \}\):

\[\begin{gather*} \frac{1}{\exp(x_i^T \theta_1 + \beta_1) + \exp(x_i^T \theta_2 + \beta_2)} \begin{bmatrix} \exp(x_i^T \theta_1 + \beta_1) \\ \exp(x_i^T \theta_2 + \beta_2) \end{bmatrix} \\[15pt] = \frac{1}{\exp((\theta_1 - \theta_2)x_i^T + \beta_1 - \beta_2) + \exp((\vec{0})x_i^T)} \begin{bmatrix} \exp((\theta_1 - \theta_2)x_i^T + \beta_1 - \beta_2) \\ \exp((\vec{0})x_i^T) \end{bmatrix} \quad \\[20pt] = \begin{bmatrix} \frac{\exp((\theta_1 - \theta_2)x_i^T + \beta_1 - \beta_2)}{1+\exp((\theta_1 - \theta_2)x_i^T + \beta_1 - \beta_2)} \\ \frac{1}{1+\exp((\theta_1 - \theta_2)x_i^T + \beta_1 - \beta_2)} \end{bmatrix} = \begin{bmatrix} 1- \frac{1}{1+\exp((\theta_1 - \theta_2)x_i^T + \beta_1 - \beta_2)} \\ \frac{1}{1+\exp((\theta_1 - \theta_2)x_i^T + \beta_1 - \beta_2)} \end{bmatrix} \end{gather*}\]

Let \(\theta^{'} = \theta_2 - \theta_1\) and \(\beta^{'} = \beta_2 - \beta_1\), we have:

\[\frac{1}{1+\exp(-(x_i^T \theta^{'} + \beta^{'}))} \space ; \quad 1 - \frac{1}{1+\exp(-(x_i^T \theta^{'} + \beta^{'}))}\]

Which denotes the probability of class 0 and 1 respectively, notice that both of the expressions above still sum up to 1. Therefore, when \(C = 2\), we only have to optimize for 1 set of weights \(\theta^{'}\) and a single bias \(\beta^{'}\). Given dataset \(X = \{ (x_i, y_i) \}_{i=1}^N\) where \(x_i \in \mathbb{R}^n\) and \(y_i \in \{ 0,1\}\), the Binary Logistic Regression model or simply Logistic Regression model is represented as:

\[P(y \mid x, \theta, \beta) = (\sigma(z))^y(1-\sigma(z))^{1-y} \space ; \quad z = x^T\theta^{'} + \beta^{'} \quad\]

• Where the weights \(\theta^{'} = \{\theta_1, \theta_2, \ldots, \theta_n\}\) and bias \(\beta^{'} \in \mathbb{R}\) are the model’s parameters.
• The expression \(\sigma(z) = \frac{1}{1+\exp(-z)}\) denotes the sigmoid function, and \(z = x^T\theta^{'} + \beta^{'}\) denotes a linear combination of the input \(x\) and the weights and bias, this function tends to \(0\) as \(z \rightarrow -\infty\) and tends to \(1\) as \(z \rightarrow +\infty\), and \(\sigma(z) + (1-\sigma(z)) = 1\).

Here is a visualization of the binary logistic regression model in the style of a neural network for queried input \(x_q\):

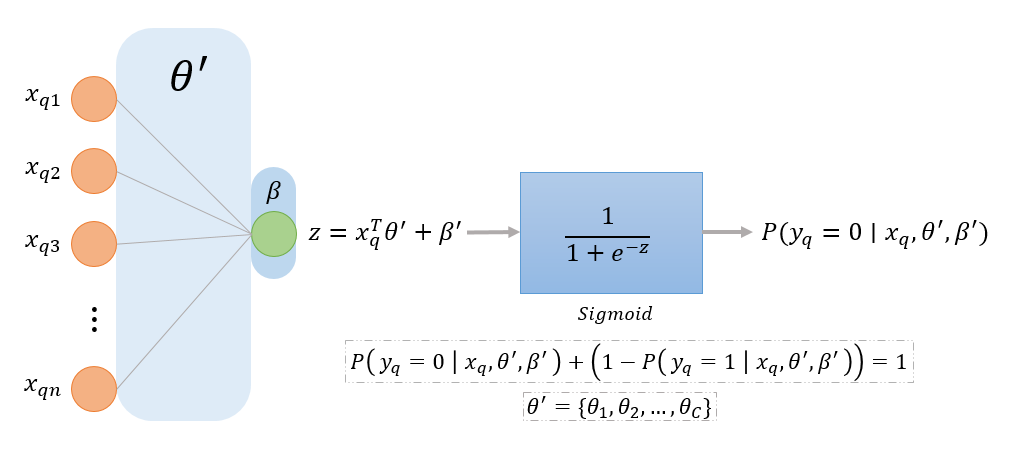
Our calculations will look a bit different:

• MLE:

\[L(\theta^{'}, \beta^{'}) = \prod_{i=1}^N P(y_i \mid x_i, \theta^{'}, \beta^{'}) \quad\]

• Log Likelihood:

\[\log L(\theta^{'}, \beta^{'}) = \sum_{i=1}^N [y_i \log \sigma (z_i) + (1 - y_i) \log (1 - \sigma(z))] \quad\]

• Cost function:

\[J(\theta^{'}, \beta^{'}) = - \frac{1}{N} \log L(\theta^{'}, \beta^{'}) \quad\]

• Gradient Descent:

\[\begin{gather*} \frac{\partial J}{\partial \theta^{'}} = -\frac{1}{N} \sum_{i=1}^N (\sigma (z_i)- y_i)x_i \quad \\[10pt] \frac{\partial J}{\partial \beta^{'}} = -\frac{1}{N} \sum_{i=1}^N (\sigma (z_i)- y_i) \\[10pt] \theta^{'\text{ new}} = \theta^{'} + \alpha \frac{\partial J}{\partial \theta^{'}} \\[10pt] \beta^{'\text{ new}} = \beta^{'} + \alpha \frac{\partial J}{\partial \beta^{'}} \end{gather*}\]

• L2 Regularization:

\[\begin{gather*} J_{\text{reg}} (\theta^{'}, \beta^{'}) = -\frac{1}{N} \log L(\theta^{'}, \beta^{'}) + \frac{1}{2N} \| \theta^{'} \|^2_2 \quad \\[10pt] \theta^{'\text{ new}} = \theta^{'} + \alpha \frac{\partial J}{\partial \theta^{'}} + \frac{1}{N} \theta^{'} \end{gather*}\]