Graph Theory I - Hoang Anh Duc - MIM - HUS - VNU

Work 1.

\[\begin{align} & \text{Given graph } G \text{ with } n { vertices and } m \text{ edges} \quad \\[5pt] & \text{Let } \Delta(G) \text{ and } \sigma(G) \text{ be the largest and smallest} \quad \\[5pt] & \text{degree of a vertex in } G \text{, respectively. Prove that:} \quad \\[5pt] & \qquad \qquad \qquad \sigma(G) \leq \frac{2m}{n} \leq \Delta(G) \end{align}\]

• Solution:

\[\begin{align} & \text{By the handshaking lemma:} \quad \\[5pt] & \sum_{v \in V(G)} \text{deg}(v) = 2m \quad \\[5pt] & \text{So the average degree is } \frac{2m}{n} \quad \\[5pt] & \text{Since deg}(v) \geq \sigma(G) \quad \forall v \quad \\[5pt] & \sum_{v \in V(G)} \text{deg}(v) \geq n \cdot \sigma(G) \implies \frac{2m}{n} \geq \sigma(G) \quad \\[5pt] & \text{Since deg}(v) \leq \Delta(G) \quad \forall v \quad \\[5pt] & \sum_{v \in V(G)} \text{deg}(v) \leq n \cdot \Delta(G) \implies \frac{2m}{n} \leq \Delta(G) \quad \\[5pt] & \text{Thus: } \sigma(G) \leq \frac{2m}{n} \leq \Delta(G) \quad \end{align}\]

Work 3.

• A regular graph is a graph where all of its vertices have the same degree. We call a graph \(n\)-regular graph if it is a regular graph which all vertices have the same degree of \(n\).

\[\begin{aligned} & \text{With what values of } n \text{ do these graphs} \quad \\[5pt] & \text{are considered regular graphs:} \quad \\[5pt] & (a) \quad K_n \quad & (c) \quad W_n \quad \\[5pt] & (b) \quad C_n \quad & (d) \quad Q_n \quad \\[5pt] \end{aligned}\]

• \(K_n\)​ (Complete graph): Each vertex connects to every other vertex. The degree of each vertex is \(n−1\), making \(K_n\)​ regular for all \(n\).
• \(C_n\)​ (Cycle graph): Each vertex in a cycle graph connects to two neighbors. The degree of every vertex is \(2\), so \(C_n\)​ is regular for all \(n \geq 3\).
• \(W_n\)​ (Wheel graph): Consists of a cycle \(C_{n−1}\)​ and a central vertex connected to all vertices of the cycle. Central vertex degree: \(n−1\). Cycle vertices degree: \(3\). Only when \(n=3\) (triangle + center), all vertices have degree \(4\), making \(W_n\)​ regular.
• \(Q_n\) ​(Hypercube graph): Each vertex connects to \(n\) others (binary representation differing by \(1\) bit). Degree is \(n\) for all vertices, so \(Q_n\) is regular for all \(n\).

Work 5.

• A simple undirected graph \(G = (V, E)\) is a bipartite graph if and only if there is a way to color each vertex of \(G\) with two colors such that no two adjacent vertices are colored the same.

• (a) Prove the statement above.

• Solution:

• To prove the statement that a graph \(G=(V,E)\) is bipartite if and only if there exists a way to color each vertex with two colors such that no two adjacent vertices are colored the same, we will prove both directions.
• Proof (If Part): Assume \(G=(V,E)\) is a bipartite graph. By definition, a bipartite graph can be partitioned into two disjoint sets \(V_1\) ​and \(V_2\), such that every edge \(e \in E\) connects a vertex in \(V_1\) ​to a vertex in \(V_2\). We can color the vertices of \(V_1\)​ with one color (say color 1) and the vertices of \(V_2\)​ with another color (say color 2). Since edges only connect vertices from \(V_1\)​ to \(V_2\), no two adjacent vertices will share the same color. Therefore, such a 2-coloring exists, proving that a bipartite graph can be 2-colored.

• Proof (Only If Part): Now, assume that there exists a 2-coloring of the vertices of \(G\) such that no two adjacent vertices share the same color. We will show that \(G\) is bipartite. Partition the vertices of \(G\) into two sets: one containing all vertices colored with color 1, and the other containing all vertices colored with color 2. Since adjacent vertices are colored differently, all edges must connect a vertex in the first set to a vertex in the second set. Thus, \(G\) is bipartite by definition. Conclusion: A graph \(G\) is bipartite if and only if there exists a way to color the vertices with two colors such that no two adjacent vertices share the same color.

• (b) Are these graphs a bipartite graph.

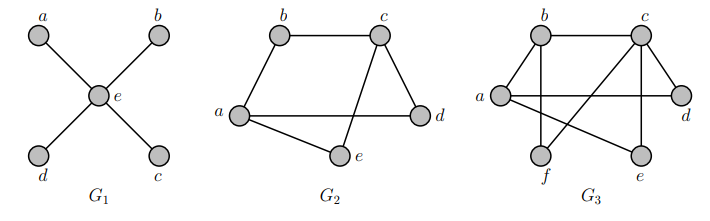
• Solution:

• \(G_1\) -> Yes
• \(G_2\) -> No (Contains cycle)
• \(G_3\) -> No (Contains cycle)

Work 6.

How many vertices and edges does these graphs have:

(a) K_n         (d) K_{m, n}
(b) C_n         (e) Q_n
(c) W_n 

• Solution:

(a) n_v = n,    n_e = (n(n-1))/2
(b) n_v = n,    n_e = n
(c) n_v = n,    n_e = 2(n-1)
(d) n_v = m+n,  n_e = m.n
(e) n_v = 2^n,  n_e = n.2^(n-1)

Work 7.

• Given a simple undirected graph \(G = (V, E)\) with \(n \geq 3\) vertices. Let \(H = (W, F)\) be a subgraph of \(G\) with at least two vertices. Prove that if \(G\) is a bipartite graph, then \(H\) is also a bipartite graph.

• Solution:

• Bipartition of \(G\): Since \(G\) is bipartite, by definition, there exists a partition of 𝑉 V into two sets \(V_1\) ​ and \(V_2\) ​ such that for every edge \((u, v) \in E\), we have \(u \in V_1\) ​ and \(v \in V_2\) ​ , or \(u \in V_2\) ​ and \(v \in V_1\).
• Subgraph \(H\): Let \(H=(W,F)\) be a subgraph of \(G\), where \(W \subset V\) and \(F \subset E\). The key observation is that the edges of \(F\) are subsets of the edges of \(G\), meaning that each edge in \(F\) connects two vertices in \(W\) and is also an edge in \(G\).
• Induced Bipartition: Since \(G\) is bipartite, its partition \((V_1 ​ ,V_2 ​ )\) induces a partition on \(W\). Specifically: Let \(W_1 ​ =W \cap V_1\) ​ be the set of vertices in \(W\) that belong to \(V_1\) ​ , Let \(W_2 ​ =W \cap V_2\) ​ be the set of vertices in \(W\) that belong to \(V_2\).
• Edges in \(F\): Any edge in \(F\) is an edge in \(G\), and since \(G\) is bipartite, each edge in \(F\) must connect a vertex in \(V_1\) ​ to a vertex in \(V_2\) ​ (since no edge in \(G\) connects two vertices within \(V_1\) ​ or within \(V_2\) ​ ).
• Conclusion: Since all edges in \(F\) must connect a vertex in \(W_1\) ​ to a vertex in \(W_2\) ​ , the set of vertices \(W\) is also bipartite, with the partition \((W_1 ​ ,W_2 ​ )\). Therefore, the subgraph \(H\) is bipartite, because its vertices can be partitioned into two sets \(W_1\) ​ and \(W_2\) ​ , with edges only between vertices in different sets.
• Thus, we have shown that if \(G\) is bipartite, then any subgraph \(H\) of \(G\) is also bipartite.

Work 11.

\[\begin{gather} \text{Suppose } G \text{ and } H \text{ are simple graphs such that} \quad \\[5pt] G \simeq H. \text{ Prove that } \overline{G} \simeq \overline{H} \quad \end{gather}\]