MAT3500 - Induction and Recursion Assignment - Part 1
29/09/2024
17
Min.
Assignment on Induction and Recursion (Part 1 - Induction)
Induction and Recursion - Hoang Anh Duc - HUS - VNU
Work 2.
- (1) Prove the following propositions using mathematical induction
\[P(n) = 1^3 + 2^3 + \ldots + n^3 = \left(\frac{n(n+1)}{2}\right)^2, \forall n \in \mathbb{Z}^+ \quad\]
- Base case: \(n = 1\)
\[\begin{gather*} LHS=1^3=1 \\[10pt] RHS=\left(\frac{1(1+1)}{2} \right)^2=1 \quad \\[10pt] \rightarrow P(1) = \mathbf{T} \end{gather*}\]
- Inductive step: Assume \(P(k) = \mathbf{T}, k \geq 1 \mid k \in \mathbb{Z}^+\)
- That is: \(1^3 + 2^3 + \ldots + k^3 = \left(\frac{k(k+1)}{2}\right)^2\)
- We need to prove: \(P(k+1) = \mathbf{T}, k \geq 1 \mid k \in \mathbb{Z}^+\)
- Which is: \(1^3 + 2^3 + \ldots + k^3 + (k+1)^3\) \(= \left(\frac{k(k+1)}{2}\right)^2 + (k+1)^3\) (inductive hypothesis)
\[\begin{flalign*} &\left(\frac{k(k+1)}{2}\right)^2 + (k+1)^3 \quad \\[5pt] = &\frac{(k(k+1))^2}{4} + \frac{4(k+1)^3}{4} \quad \\[5pt] = &\frac{(k(k+1))^2+4(k+1)^3}{4} \quad \\[5pt] = &(k+1)^2\left(\frac{k^2+4k+4}{4}\right) \quad \\[5pt] = &\left(\frac{(k+1)(k+2)}{4}\right)^2 \end{flalign*}\]
- So \(P(k+1) = \mathbf{T}, k \geq 1 \mid k \in \mathbb{Z}^+\)
- By induction, \(P(n) = \mathbf{T}, \forall n \in \mathbb{Z}^+\)
- (2) Prove the following propositions using mathematical induction
\[P(n) = 1^2 + 3^2 + 5^2 + \ldots + (2n+1)^2 = \frac{(n+1)(2n+1)(2n+3)}{3}, \forall n \in \mathbb{N} \quad\]
- Base case: \(n = 0\)
\[\begin{flalign*} LHS&=(2\cdot 0+1)^2=1 \\[10pt] RHS&=\frac{(0+1)(2\cdot 0+1)(2\cdot 0+3)}{3} \quad \\[10pt] &=\frac{1\cdot 1\cdot 3}{3}=1 \quad \\[10pt] &\rightarrow P(0) = \mathbf{T} \end{flalign*}\]
- Inductive step: Assume \(P(k) = \mathbf{T}, k \geq 0 \mid k \in \mathbb{N}\)
- That is: \(1^2 + 3^2 + 5^2 + \ldots + (2k+1)^2\) \(= \frac{(k+1)(2k+1)(2k+3)}{3}\)
- We need to prove: \(P(k+1) = \mathbf{T}, k \geq 0 \mid k \in \mathbb{N}\)
- Which is:
\[\begin{flalign*} & 1^2 + 3^2 + 5^2 + \ldots + (2k+1)^2 + (2(k+1)+1)^2 \quad \\[8pt] &= \frac{(k+1)(2k+1)(2k+3)}{3} + (2(k+1)+1)^2 \quad \\[8pt] &\text{(By the inductive hypothesis)} \end{flalign*}\]
- We have:
\[\begin{flalign*} &\frac{(k+1)(2k+1)(2k+3)}{3} + (2(k+1)+1)^2 \quad \\[5pt] = &\frac{(k+1)(2k+1)(2k+3) + 3(2k+3)^2}{3} \quad \\[5pt] = &\frac{(2k+3)\left[(k+1)(2k+1)+3(2k+3)\right]}{3} \quad \\[5pt] = &\frac{(2k+3)\left[2k^2+3k+1+6k+9\right]}{3} \quad \\[5pt] = &\frac{(2k+3)\left[2k^2+9k+10\right]}{3} \quad \\[5pt] = &\frac{(2k+3)\left[2k^2+5k+4k+10\right]}{3} \quad \\[5pt] = &\frac{(2k+3)(k+2)(2k+5)}{3} \quad \\[5pt] \end{flalign*}\]
- So \(P(k+1) = \mathbf{T}, k \geq 0 \mid k \in \mathbb{N}\)
- By induction, \(P(n) = \mathbf{T}, \forall n \in \mathbb{N}\)
- (3) Prove the following propositions using mathematical induction
\[P(n) = 3 + 3 \cdot 5 + 3 \cdot 5^2 + \ldots + 3 \cdot 5^n = \frac{3(5^{n+1}-1)}{4}, \forall n \in \mathbb{N} \quad\]
- Base case: \(n = 0\)
\[\begin{flalign*} LHS&=3\cdot5^0=3 \\[10pt] RHS&=\frac{3(5^{0+1}-1)}{4} \quad \\[10pt] &=\frac{3\cdot 4}{4}=3 \quad \\[10pt] & \rightarrow P(0) = \mathbf{T} \end{flalign*}\]
- Induction step: Assume \(P(k) = \mathbf{T}, k \geq 0 \mid k \in \mathbb{N}\)
- That is: \(3 + 3 \cdot 5 + 3 \cdot 5^2 + \ldots + 3 \cdot 5^k\) \(= \frac{3(5^{k+1}-1)}{4}\)
- We need to prove: \(P(k+1) = \mathbf{T}, k \geq 0 \mid k \in \mathbb{N}\)
- Which is:
\[\begin{flalign*} & 3 + 3 \cdot 5 + 3 \cdot 5^2 + \ldots + 3 \cdot 5^k + 3 \cdot 5^{k+1} \quad \\[8pt] &= \frac{3(5^{k+1}-1)}{4} + 3 \cdot 5^{k+1} \text{ (Inductive hypothesis)} \end{flalign*}\]
- We have:
\[\begin{flalign*} &\frac{3(5^{k+1}-1)}{4} + 3 \cdot 5^{k+1} \quad \\[5pt] = &\frac{3(5^{k+1}-1)+3\cdot 4\cdot 5^{k+1}}{4} \quad \\[5pt] = &\frac{3\cdot 5^{k+1}-3+3\cdot 4\cdot 5^{k+1}}{4} \quad \\[5pt] = &\frac{3\cdot 5^{k+1}(1+4)-3}{4} \quad \\[5pt] = &\frac{3\cdot 5^{k+1}\cdot 5-3}{4} \quad \\[5pt] = &\frac{3\cdot 5^{k+2}-3}{4} \quad \\[5pt] = &\frac{3(5^{k+2}-1)}{4} \quad \\[5pt] \end{flalign*}\]
- So \(P(k+1) = \mathbf{T}, k \geq 0 \mid k \in \mathbb{N}\)
- By induction, \(P(n) = \mathbf{T}, \forall n \in \mathbb{N}\)
Work 3.
- (1) Prove the following propositions
\[\text{Prove: P(n) = } 3^n < n!, \forall n > 6 \mid n \in \mathbb{Z} \quad\]
- Base case: \(n = 7\)
- We have: \(LHS = 3^7 = 2187\)
- We have: \(RHS = 7! = 5040\)
- Since: \(2187 < 5040\), therefore: \(P(7) = \mathbf{T}\)
- Induction step: Assume \(P(k) = \mathbf{T}, k > 6 \mid k \in \mathbb{Z}\)
- That is: \(3^k < k!\)
- We need to prove: \(P(k+1) = \mathbf{T}, k > 6 \mid k \in \mathbb{Z}\)
- Which is:
\[\begin{flalign*} & 3^{k+1} < (k+1)! \quad \\[5pt] & \equiv 3 \cdot 3^k < (k+1)k! \quad \\[5pt] & \equiv 3^k < \frac{k+1}{3}k! \quad \\[5pt] & \text{For } k > 6 \mid k \in \mathbb{Z}: \quad \\[5pt] & k! < \frac{k+1}{3}k! \quad \\[5pt] & \text{From the inductive hypothesis,} \quad \\[5pt] & \text{We know that } 3^k < k! \text{ so:} \quad \\[5pt] & 3^k < \frac{k+1}{3}k!, k > 6 \mid k \in \mathbb{Z} \quad \end{flalign*}\]
- Therefore \(P(k+1) = \mathbf{T}, k > 6 \mid k \in \mathbb{Z}\)
- By induction, \(P(n) = \mathbf{T}, \forall n > 6 \mid n \in \mathbb{Z}\)
- (2) Prove the following propositions
\[\begin{gather*} \text{With what value of positive integer n does:} \quad \\[6pt] P(n) = 2n + 3 \leq 2^n \text{ holds True?} \quad \\[6pt] \text{Give your reasoning} \end{gather*}\]
- For \(n = 1\):
\[\begin{align} & 2\cdot 1 + 3 \leq 2^1 \quad \\ & 5 \leq 2 = \mathbf{F} \quad \\ \end{align}\]
- For \(n = 2\):
\[\begin{align} & 2\cdot 2 + 3 \leq 2^2 \quad \\ & 7 \leq 4 = \mathbf{F} \quad \\ \end{align}\]
- For \(n = 3\):
\[\begin{align} & 2\cdot 3 + 3 \leq 2^3 \quad \\ & 9 \leq 8 = \mathbf{F} \quad \\ \end{align}\]
- For \(n = 4\):
\[\begin{align} & 2\cdot 4 + 3 \leq 2^4 \quad \\ & 15 \leq 16 = \mathbf{T} \quad \\ \end{align}\]
- We found our base case of \(n = 4\)
- Induction step: Assume \(P(k) = \mathbf{T}, k > 3 \mid n \in \mathbb{Z}\)
- That is: \(2k+3 \leq 2^k\)
- We need to prove: \(P(k+1) = \mathbf{T}, k > 3 \mid k \in \mathbb{Z}\)
- Which is:
\[\begin{flalign*} & 2(k+1)+3 \leq 2^{k+1} \quad \\[5pt] & \equiv 2k+3+2 \leq 2\cdot 2^k \quad \\[5pt] & \equiv 2k+3 \leq 2\cdot 2^k-2 \quad \\[5pt] & \text{For } k > 3 \mid k \in \mathbb{Z}: \quad \\[5pt] & 2^k < 2\cdot 2^k -2 \quad \\[5pt] & \text{From the inductive hypothesis,} \quad \\[5pt] & \text{We know that } 2k+3 \leq 2^k \text{ so:} \quad \\[5pt] & 2k+3 < 2\cdot 2^k-2, k > 3 \mid k \in \mathbb{Z} \quad \end{flalign*}\]
- Therefore \(P(k+1) = \mathbf{T}, k > 3 \mid k \in \mathbb{Z}\)
- By induction, \(P(n) = \mathbf{T}, \forall n > 3 \mid n \in \mathbb{Z}\)
- Therefore, the smallest value of positive integer \(n\) for which \(P(n) = \mathbf{T}\) is \(n = 4\)
- (3) Prove the following propositions
\[\text{Prove that P(n) = } n^3 + 2n \space \vdots \space 3, \forall n \in \mathbb{Z}^+ \quad\]
- Base case: \(n = 1\)
- We have: \(1^3 + 2 \cdot 1 = 3 \space \vdots \space 3\)
- Therefore: \(P(1) = \mathbf{T}\)
- Induction step: Assume \(P(k) = \mathbf{T}, k \geq 1 \mid k \in \mathbb{Z}^+\)
- That is: \(k^3 + 2k \space \vdots \space 3\)
- We need to prove: \(P(k+1) = \mathbf{T}, k \geq 1 \mid k \in \mathbb{Z}^+\)
- Which is:
\[\begin{flalign*} & (k+1)^3+2(k+1)\quad \\[5pt] & = k^3+3k^2+3k+2k+3 \quad\\[5pt] & = (k^3+2k)+(3k^2+3k+3) \quad\\[5pt] & (3k^2+3k+3) \text{ trivially } \vdots \space 3 \quad \\[5pt] & \text{We know that } k^3 + 2k \space \vdots \space 3 \text{ so:} \quad \\[5pt] & (k^3+2k)+(3k^2+3k+3) \space \vdots \space 3, k \geq 1 \mid k \in \mathbb{Z}^+ \quad \\[5pt] & \text{Therefore } (k+1)^3+2(k+1) \space \vdots \space 3, k \geq 1 \mid k \in \mathbb{Z}^+ \end{flalign*}\]
- Therefore \(P(k+1) = \mathbf{T}, k \geq 1 \mid k \in \mathbb{Z}^+\)
- By induction, \(P(n) = \mathbf{T}, \forall n \in \mathbb{Z}^+\)
Work 4.
- Prove the following proposition using mathematical induction:
\[P(n) = \sum_{i=0}^{n} 2^i = 2^{n+1} - 1 , \forall n \geq 0 \mid n \in \mathbb{Z} \quad\]
- Base case: \(n = 0\)
\[\sum_{i=0}^{0} 2^i = 2^0 = 1 = 2^{0+1} - 1 = RHS \quad\]
- Therefore: \(P(0) = \mathbf{T}\)
- Induction step: Assume \(P(k) = \mathbf{T}, k \in \mathbb{Z}^+\)
\[\sum_{i=0}^{k} 2^i = 2^{k+1} - 1 \quad\]
- We need to prove: \(P(k+1) = \mathbf{T}, k \in \mathbb{Z}^+\)
\[\begin{align} \sum_{i=0}^{k+1} 2^i &= 2^{(k+1)+1} - 1 = 2^{k+2}-1 \quad \\[8pt] \text{From the } &\text{inductive hypothesis, we have:} \quad \\[6pt] \sum_{i=0}^{k+1} 2^i &= \left(\sum_{i=0}^{k} 2^i\right) + 2^{k+1} \quad \\[8pt] \sum_{i=0}^{k+1} 2^i &= (2^{k+1}-1) + 2^{k+1} \quad \\[8pt] \sum_{i=0}^{k+1} 2^i &= 2\cdot 2^{k+1}-1 \quad \\[8pt] \sum_{i=0}^{k+1} 2^i &= 2^{k+2}-1 \end{align}\]
- Therefore \(P(k+1) = \mathbf{T}, k \in \mathbb{Z}^+\)
- By induction, \(P(n) = \mathbf{T}, \forall n \in \mathbb{Z}^+\)
Work 5.
- Prove the following proposition using mathematical induction:
\[P(n) = 2^n \geq n^2 , \forall n \geq 4 \mid n \in \mathbb{Z} \quad\]
- Base case: \(n = 4\)
- We have: \(2^4 = 16 \geq 16 = 4^2\)
- Therefore: \(P(4) = \mathbf{T}\)
- Induction step: Assume \(P(k) = \mathbf{T}, k \geq 4 \mid n \in \mathbb{Z}\)
- That is: \(2^k \geq k^2\)
- We need to prove: \(P(k+1) = \mathbf{T}, k \geq 4 \mid n \in \mathbb{Z}\)
- Which is:
\[\begin{flalign*} & 2^{k+1} \geq (k+1)^2 \quad \\[5pt] & \equiv 2 \cdot 2^k \geq k^2+2k+1 \\[5pt] & \equiv 2^k \geq \frac{1}{2}k^2 + k + \frac{1}{2} \quad \\[5pt] & \text{For } k \geq 4 \mid k \in \mathbb{Z}: \quad \\[8pt] & k^2 \geq \frac{k^2}{2} + k + \frac{1}{2} \quad \\[8pt] & \equiv k^2 + 2k + 1 \geq 0 \quad \\[5pt] & \text{Which is True because RHS is an increasing} \quad \\[2pt] & \text{quadratic with global minima 0} \quad \\[5pt] & \text{From the inductive hypothesis,} \quad \\[5pt] & \text{We know that } 2^k \geq k^2 \text{ so:} \quad \\ & 2^k \geq \frac{1}{2}k^2 + k + \frac{1}{2}, \forall k \geq 4 \mid k \in \mathbb{Z} \quad \end{flalign*}\]
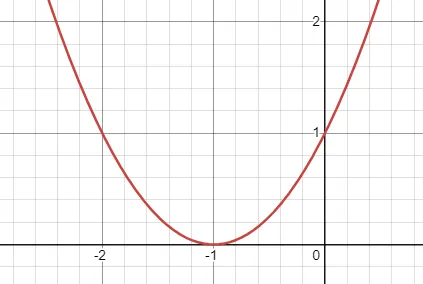
$$ k^2 + 2k + 1 $$
- Therefore \(P(k+1) = \mathbf{T}, k \geq 4 \mid k \in \mathbb{Z}\)
- By induction, \(P(n) = \mathbf{T}, \forall n \geq 4 \mid n \in \mathbb{Z}\)
Work 7.
- Prove the following proposition:
\[\begin{gather*} \text{For all } n \geq 2 \mid n \in \mathbb{Z} \quad \\ \text{The sets } A_1,A_2,\ldots,A_n \text{ satisfies:} \quad \\ \overline{A_1 \cap A_2 \cap \ldots \cap A_n} = \overline{A_1} \cup \overline{A_2} \cup \ldots \cup \overline{A_n} \quad \end{gather*}\]
- First we define the proposition above as P(n).
- We will use De Morgan’s Laws and Induction:
\[\begin{gather} \text{De Morgan's Laws} \quad \\[8pt] \overline{A \cap B} = \overline{A} \cup \overline{B} \quad \\[5pt] \overline{A \cup B} = \overline{A} \cap \overline{B} \quad \end{gather}\]
- Base case: \(n = 2 \mid \overline{A_1 \cap A_2}\) \(= \overline{A_1} \cup \overline{A_2}\)
- By De Morgan’s Law: \(P(n) = \mathbf{T}\)
- Induction step: Assume \(P(k) = \mathbf{T}, k \geq 2 \mid k \in \mathbb{Z}\)
- That is \(\overline{A_1 \cap A_2 \cap \ldots \cap A_k}\) \(= \overline{A_1} \cup \overline{A_2} \cup \ldots \cup \overline{A_k}\)
- We need to prove: \(P(k+1) = \mathbf{T}, k \geq 2 \mid k \in \mathbb{Z}\)
- Which is: \(\overline{A_1 \cap A_2 \cap \ldots \cap A_{k+1}}\) \(= \overline{A_1} \cup \overline{A_2} \cup \ldots \cup \overline{A_k} \cup \overline{A_{k+1}}\)
- Consider: \(A_1 \cap A_2 \cap \ldots \cap A_{k+1}\) \(= (A_1 \cap A_2 \cap \ldots \cap A_k) \cap A_{k+1}\)
\[\begin{align} & \text{With } A_1 \cap A_2 \cap \ldots \cap A_{k+1} = (A_1 \cap A_2 \cap \ldots \cap A_k) \cap A_{k+1} \quad \\[5pt] & \text{Take the complement of RHS, by De Morgan's Law:} \quad \\[5pt] & \overline{(A_1 \cap A_2 \cap \ldots \cap A_k) \cap A_{k+1}} = \overline{(A_1 \cap A_2 \cap \ldots \cap A_k)} \cup \overline{A_{k+1}} \quad \\[5pt] & \text{From the inductive hypothesis:} \quad \\[5pt] & \overline{(A_1 \cap A_2 \cap \ldots \cap A_k)} \cup \overline{A_{k+1}} = \overline{A_1} \cup \overline{A_2} \cup \ldots \cup \overline{A_k} \cup \overline{A_{k+1}} \quad \\[5pt] \end{align}\]
- Therefore \(P(k+1) = \mathbf{T}, k \geq 2 \mid k \in \mathbb{Z}\)
- By induction, \(P(n) = \mathbf{T}, \forall n \geq 2 \mid n \in \mathbb{Z}\)
Work 9.
- Prove the followings:
\[\begin{align} & \text{With sets } A_1,A_2,\ldots,A_n \text{ and } B, n \geq 2 \mid n \in \mathbb{Z} \quad \\[5pt] & \text{Prove the following propositions:} \quad \\[8pt] & (a) \space (A_1 \cap A_2 \cap \ldots \cap A_n) \cup B = (A_1 \cup B) \cap (A_2 \cup B) \cap \ldots \cap (A_n \cup B) \quad \\[5pt] & (b) \space (A_1 \cup A_2 \cup \ldots \cup A_n) \cap B = (A_1 \cap B) \cup (A_2 \cap B) \cup \ldots \cup (A_n \cap B) \quad \\[5pt] & (c) \space (A_1 - B) \cap (A_2 - B) \cap \ldots \cap (A_n - B) = (A_1 \cap A_2 \cap \ldots \cap A_n) - B \quad \\[5pt] & (d) \space (A_1 - B) \cup (A_2 - B) \cup \ldots \cup (A_n - B) = (A_1 \cup A_2 \cup \ldots \cup A_n) - B \quad \\[5pt] \end{align}\]
- (a) and (b): Similar to Work 7. using Distributive Laws and Induction.
- (c) is similar to (d), so I will demonstrate with (c).
\[(c) \space (A_1 - B) \cap (A_2 - B) \cap \ldots \cap (A_n - B) = (A_1 \cap A_2 \cap \ldots \cap A_n) - B \space , n \geq 2 \mid n \in \mathbb{Z} \quad\]
- First we define the proposition above as P(n).
- Base case: \(n = 2 \mid (A_1 - B) \cap (A_2 - B)\) \(= (A_1 \cap A_2) - B\). Proof:
\[\begin{align} & \text{Let x } \in (A_1 - B) \cap (A_2 - B) \quad \\[5pt] & \rightarrow (x \in A_1 - B) \wedge (x \in A_2 - B) \quad \\[5pt] & \rightarrow (x \in A_1) \wedge (x \in A_2) \wedge (x \notin B) \quad \\[5pt] & \rightarrow x \in A_1 \cap A_2 \quad \\[5pt] & (x \notin B) \rightarrow x \in (A_1 \cap A_2) - B \quad \\[10pt] & \text{Therefore } (A_1 - B) \cap (A_2 - B) \subseteq (A_1 \cap A_2) - B \quad \\[30pt] & \text{Let x } \in (A_1 - B) \cap (A_2 - B) \quad \\[5pt] & \rightarrow (x \in A_1 \cap A_2) \wedge (x \notin B) \quad \\[5pt] & \rightarrow (x \in A_1) \wedge (x \in A_2) \quad \\[5pt] & (x \notin B) \rightarrow (x \in A_1 - B) \wedge (x \in A_2 - B) \quad \\[5pt] & \rightarrow x \in (A_1 - B) \cap (A_2 - B) \quad \\[10pt] & \text{Therefore } (A_1 \cap A_2) - B \subseteq (A_1 - B) \cap (A_2 - B) \end{align}\]
- Induction step: Assume \(P(k) = \mathbf{T}, k \geq 2 \mid k \in \mathbb{Z}\)
- That is \((A_1 - B) \cap (A_2 - B) \cap\) \(\ldots \cap (A_k - B)\) \(= (A_1 \cap A_2 \cap \ldots \cap A_k) - B\)
- We need to prove: \(P(k+1) = \mathbf{T}, k \geq 2 \mid k \in \mathbb{Z}\)
- Which is:
\[\begin{align} & (A_1 - B) \cap (A_2 - B) \cap \ldots \cap (A_k - B) \cap (A_{k+1} - B) \quad \\[5pt] & \text{From the inductive hypothesis,} \quad \\[5pt] & = ((A_1 \cap A_2 \cap \ldots \cap A_k) - B) \cap (A_{k+1} - B) \quad \\[5pt] & = (A_1 \cap A_2 \cap \ldots \cap A_k \cap A_{k+1}) - B \quad \\[5pt] \end{align}\]
- Therefore \(P(k+1) = \mathbf{T}, k \geq 2 \mid k \in \mathbb{Z}\)
- By induction, \(P(n) = \mathbf{T}, \forall n \geq 2 \mid n \in \mathbb{Z}\)
Work 11.
- Prove the following using mathematical induction:
\[\begin{gather} \text{Define } p_1,\ldots ,p_n \text{ as logical proposition and } n \geq 2 \mid n \in \mathbb{Z} \text{ prove:} \quad \\[5pt] \neg(p_1 \vee p_2 \vee \ldots \vee p_n) = \neg p_1 \wedge \neg p_2 \wedge \ldots \wedge \neg p_n \quad \end{gather}\]
- This is similar to Work 7.
- \(\neg p_k\) is essentially \(\overline{A_k}\)
- \(\cup, \cap\) are essentially \(\vee, \wedge\)
- We can solve this problem using De Morgan’s Laws and Induction.
Work 13.
- Prove the followings:
\[\begin{align} & \text{Define } P(n) = \exists \space a, b \in \mathbb{Z} \mid n = 3a + 5b \quad \\[5pt] & \text{This problem demonstrate Strong Induction by proving} \quad \\[5pt] & \text{P(n) when } n \geq 8 \text{ , follow these steps:} \quad \\[8pt] & (1) \text{ Prove for } P(8), P(9), P(10) \text{ to from the base case} \quad \\[5pt] & (2) \text{ Find the inductive hypothesis}\quad \\[5pt] & (3) \text{ Formulate the induction step}\quad \\[5pt] & (4) \text{ Complete the inductive process with } n \geq 10 \end{align}\]
\[\begin{align} & \text{(1) Base cases:} \quad \\[15pt] & P(8) = 3(1) + 5(1) = \mathbf{T} \quad \\[5pt] & P(9) = 3(3) + 5(0) = \mathbf{T} \quad \\[5pt] & P(10) = 3(0) + 5(2) = \mathbf{T} \quad \\[5pt] \end{align}\]
\[\begin{align} & \text{(2) Inductive hypothesis:} \quad \\[15pt] & \text{Assume } P(k) = \mathbf{T}, \forall k \mid 8 \leq k \leq n, \text{ for some } n \geq 10 \quad \\[5pt] & \rightarrow \forall k \mid 8 \leq k \leq n, \exists a,b \in \mathbb{Z} \mid k=3a+5b \quad \\[5pt] \end{align}\]
\[\begin{align} & \text{(3) Induction step:} \quad \\[15pt] & \text{We need to prove: } P(k+1) = \mathbf{T}, \forall k \mid 8 \leq k \leq n, \text{ for some } n \geq 10 \quad \\[5pt] & \text{Consider } n+1 \quad \\[5pt] & \text{For some } n+1 \geq 11 \mid n + 1 = (n - 2) + 3 \quad \\[5pt] & \text{Since } n \geq 10 \rightarrow n - 2 \geq 8 \quad \\[5pt] & \text{By the inductive hypothesis: } P(n-2) = \mathbf{T} \rightarrow n-2 = 3a+5b, a,b \in \mathbb{Z} \quad \\[5pt] & \text{Then: } n + 1 = (n - 2) + 3 = 3a +5b + 3 = 3(a+1) + 5 \quad \\[5pt] & \rightarrow n + 1 = 3a'+5b',a',b'\in \mathbb{Z} \mid a'=a+1,b'=b \quad \\[5pt] & \rightarrow P(n+1) = \mathbf{T} \end{align}\]
\[\begin{align} & \text{(4) Conclude inductive process:} \quad \\[15pt] & \text{We've shown: } P(k) = \mathbf{T}, \forall k \mid 8 \leq k \leq n, \text{ for some } n \geq 10 \quad \\[5pt] & \text{And also: } P(n+1) = \mathbf{T}, \forall k \mid 8 \leq k \leq n, \text{ for some } n \geq 10 \quad \\[5pt] & \text{By the principal of Strong Induction } P(n) = \mathbf{T}, \forall n \geq 8 \mid n \in \mathbb{Z} \end{align}\]
Work 17.
- Prove the followings:
\[\begin{align} & \text{Given } s \in S \text{ and } t \in S \text{ as sets of positive integers} \quad \\[5pt] & \text{Prove that S is defined by } 1 \in S \text{ and } s+t \in S \\[5pt] & (\text{Hint: Prove that } S \subseteq \mathbb{Z}^+ \text{ and } \mathbb{Z}^+ \subseteq S ) \end{align}\]
- First we define the proposition above as P(n).
- Since \(1 \in S \rightarrow S \subseteq \mathbb{Z}^+\) (*)
- We need to prove: \(\mathbb{Z}^+ \subseteq S\)
- Base case: \(n = 1 \mid P(1)\) \(= \mathbf{T} \text{ (Proven above in (*))}\)
- Inductive step: Assume \(k \in S, k\) \(\leq n \mid k,n \in \mathbb{Z}^+\)
- We need to prove: \(n + 1 \in S\)
- We have \((n \in S) \wedge (1 \in S) \rightarrow n+1 \in S\)
- By induction, \(\mathbb{Z}^+ \subseteq S\)
- Since \(S \subseteq \mathbb{Z}^+\) and \(\mathbb{Z}^+ \subseteq S\)
- We conclude \(S = \mathbb{Z}^+\)
- References and Extras:
- Work 17. Complement.
- Work 17. Complement.
- Work 9. Complement.
- Mary Radckiffe, Carnegie Mellon University - Induction
- David A. Cox, Catherine C. McGeoch, Amherst College - Logic, Sets, and Proofs
- Kenneth H. Rosen - Discrete Mathematics and Its Applications.